一种基于预设的形状记忆合金驱动器反步滑模控制方法

本发明涉及自动控制，特别是涉及一种基于预设的形状记忆合金驱动器反步滑模控制方法。

背景技术：

1、形状记忆合金材料凭借其卓越的变形能力、较高的输出力与质量比、小巧的尺寸、轻量化的特性以及低噪音的变形过程，在航空工程、精密制造及生物医疗等领域显示出广阔的应用潜力，该材料因具备在特定温度或压力下展现出的形状记忆效应，吸引了众多研究者的深入探索。近年来，形状记忆合金材料在驱动装置中的应用逐渐成为研究热点，该材料具备高机械性能、紧凑轻便的特点使其能够轻松地集成到小尺寸机械装置中，作为驱动元件发挥关键作用，进一步拓展了其在实际应用中的价值。当使用sma导线作为驱动元件时，相比较电机驱动器，其优点是通过材料收缩行为产生直线运动，可以对驱动机构进行轻量化和小型化设计。

2、通过深入研究形状记忆合金驱动器的控制技术和应用领域，可以有效改善驱动过程中的应力非线性变化行为，实现精确控制，提高系统的响应精度和稳定性。此外，形状记忆合金驱动器在医疗、工程、航空航天、电子和能源等领域具有广泛的应用前景，能够为人类社会的科技进步和产业发展提供有力的支持。因此，对形状记忆合金驱动器的研究不仅具有理论价值，还具有广阔的应用前景和巨大的经济价值。

3、目前对于形状记忆合金驱动器的研究包含材料学和控制器两个方面：

4、尽管通过焦耳加热等方式能够较为容易地实现形状记忆合金材料的加热与驱动，但sma驱动器中的材料应变对输入电流的非线性响应是其主要的问题。sma表现出的迟滞特性最终导致控制的精度问题，因此精准控制其行为仍面临挑战。为了提升控制精度，研究者们或是努力构建更为精准的模型以全面反映材料在各种工况下的动力学特性，或是设计能够有效抑制建模误差的控制器。然而不侧重材料的物理机理上研究sma的力学行为，而只采用较少的内变量和材料参数即可简单高效地描述sma的形状记忆效应和超弹性特性的模型有很多，主要可以分为本构模型和唯象模型，又因其本构模型的简便性、高效性和实用性，使其成为研究者更倾向选择的建模方法。

5、为了提高形状记忆合金驱动器的控制精度，大多数研究者会从控制器方面着手研究，例如工业控制与经典的pid控制策略，但常规的pid控制策略并不适应在形状记忆合金材料中，因为其具有非线性迟滞的特征。因此大多数研究均采用改进型的pid控制策略，如双线性补偿器、滑模变结构、卡尔曼滤波器、模糊控制器以及神经网络控制方法等。上述方法虽然可以实现较好的系统控制效果，但在控制器设计的过程中，并未充分考虑到系统的瞬态性能，而预设性能控制方法则通过将误差转换为无约束误差，并严格将其限制在预设的性能包络之内，从而在确保系统稳态性能的同时，能够显著地提升系统的瞬态性能，进而优化系统整体的控制效果。

技术实现思路

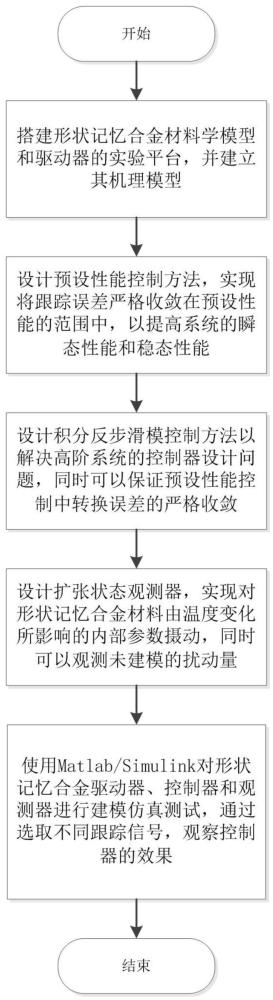
1、本发明的目的在于提供一种基于预设的形状记忆合金驱动器反步滑模控制方法，本发明为一种基于预设性能控制的预设性能控制的形状记忆合金驱动器输出角度的积分反步滑模控制方法，解决了形状记忆合金材料在驱动过程中由于非线性、动作迟滞、参数时变等因素导致的控制精度不佳的问题。

2、本发明采用如下技术方案：

3、一种基于预设的形状记忆合金驱动器反步滑模控制方法，所述方法包括以下步骤：

4、s1，搭建的实验平台，并建立其机理模型，得到其控制系统状态空间方程；

5、s2，设计扩张状态观测器，观测并补偿形状记忆合金材料在温度变化引起的

6、参数摄动问题，还用以观测系统未建模的扰动量；

7、s3，基于材料学和机理模型，设计预设性能控制方法；通过人为设定预设的性能包络ρ，将系统的跟踪误差e1严格限制在预设性能范围内，从而确保系统具有较高的响应速度和稳态特性；

8、s4，为确保预设性能控制中转换误差μ的有界性，设计积分滑模反步控制方法，同时实现了三阶系统的控制器设计；

9、s5，对上述控制器进行稳定性分析，并对转换误差进行有界性分析；

10、s6，使用matlab/simulink对形状记忆合金驱动器、控制器和观测器进行仿真测试，观察驱动器输出角度的稳定性。

11、所述的一种基于预设的形状记忆合金驱动器反步滑模控制方法，所述搭建形状记忆合金材料学模型和驱动器的模型，材料学模型由三个部分组成，即本构模型、相变模型和热力学模型；

12、s11，本构模型

13、本构模型反应温度t、应力σ、应变ε与马氏体体积分数ξ之间的关系；

14、

15、其中，为应力速率；为应变速率；为马氏体体积分数变化速率；为温度变化速率；e为材料的弹性模量；ω为相变系数；θ为热传递系数；

16、e＝ea+ξ(em-ea)

17、其中，ea和em分别为奥氏体和马氏体的弹性模量；

18、ω＝-εre

19、εr为最大可恢复应变；

20、s12，相变模型

21、相变模型是描述sma在加热和冷却过程中马氏体体积分数的变化；

22、加热过程：从低温马氏体相变化为高温奥氏体相；

23、

24、冷却过程：从高温奥氏体相变化为低温马氏体相。

25、

26、其相变过程最终推导出马氏体体积分数的变化。式中ξ0为初始状态的马氏体体积分数，aa、am、ba、bm分别为sma材料的相关常数，其计算如下：

27、

28、

29、其中，ms、mf、as、af分别代表sma马氏体起始、终止温度和奥氏体起始、终止温度。cm和ca分别表示在温度为af和mf时的sma材料应力和温度之间的一阶导数。

30、s13，热力学模型

31、热力学模型主要描述sma在加热过程中，由电压升高而引起的温度变化；根据热力学第一定律[32]，sma的温度变化关系式为：

32、

33、其中，m、cp、v、r、h、aw、t0分别为sma材料的质量、比热系数、输入电压、电阻、传热系数、横截面积和环境温度。

34、由于sma加热或冷却过程中材料电阻r不是固定值，而随着相变规律变化，其关系式为：

35、r＝ra+(rm-ra)ξ

36、传热系数h与材料温度t相关，其关系式如下：

37、h＝h0+h2t2

38、其中，rm、ra分别为sma在马氏体和奥氏体状态的内阻；h0、h2分别为零阶和二阶传热系数。

39、s14，驱动器机理模型

40、如图2所示为sma驱动器机理模型简图，sma驱动器模型主要由固定端、偏置驱动器和输出端组成，其中偏置驱动器由弹簧和sma丝构成，偏置驱动器连接固定端和输出装置。当sma丝通电加热时，其材料因形状记忆效应而产生拉力。当拉力超过弹簧的弹力，输出装置的角度便会发生相应的变化。然而，当sma丝冷却时，它会逐渐恢复到初始长度，从而带动输出角度回归至原始状态。根据扭矩平衡原理建立角度-力矩的动力学模型。

41、

42、i、c、k分别为转动惯量、扭转阻尼系数和弹簧的弹性系数；θ为驱动器物体的转动角度；为转动角速度；为转动角加速度；fsma为形状记忆合金丝输出力；fsma与sma输出应力关系为：

43、fsma＝σaw

44、其中，驱动器物体的转动角度与sma丝应变相关，其运动学关系式为：

45、εl＝aθ

46、其中，l、a分别为sma的长度和物体距转轴的距离。

47、将输出力与应力关系代入动力学模型后得到应力与角度的二阶关系式：

48、

49、为了进一步得到电压与输出角度的关系，将上式求导得到角度和应力的关系：

50、

51、将本构关系模型代入上式后得到：

52、

53、随后分别代入运动学模型和热力学模型后得到：

54、

55、为简化计算，令中间变量h和n为：

56、h＝haw(t-t0)

57、

58、则可以得到电压v与角度θ的三阶关系式：

59、

60、综上、推导得出输入电压与驱动器输出角度的三阶系统。

61、s15，建立控制系统

62、根据三阶系统表达式，令x1＝θ、u＝v2

63、

64、为简化状态空间方程表达式，令：

65、

66、

67、随后建立控制系统的状态空间方程:

68、

69、其中d为系统未建模扰动量。

70、所述的一种基于预设的形状记忆合金驱动器反步滑模控制方法，所述扩张状态观测器来实现对形状记忆合金材料由于温度变化引起的参数摄动的观测，同时还可以观测系统中未建模的扰动量d，其构建扩张状态观测器步骤如下：

71、

72、将非线性函数fal取为：

73、

74、其中，η1为x3的观测值、而η2为d的观测值其中β1、β2>0；α1、α2、为非线性函数fal的控制参数，σ1为观测误差。

75、所述的一种基于预设的形状记忆合金驱动器反步滑模控制方法，所述预设性能控制，其设计过程是将系统误差收敛至一个预设的性能包络内，保证其最小收敛速度在预设性能中，且最大超调也不能超过预设性能，即可保证系统的瞬态性能；其具体设计步骤如下：

76、s41，定义误差

77、首先，定义sma驱动器输出角度误差e1(t)；

78、e1(t)＝x1-x1d

79、s42，设计性能函数

80、通过性能函数来构造预设性能边界，性能函数需要满足

81、(1)性能函数ρ(t)在定义的时间域内恒正且单调递减；

82、(2)当时，ρ∞>0。

83、因此可以设计为

84、ρ(t)＝(ρ0-ρ∞)e-pt+ρ∞

85、其中，ρ0，ρ∞和p为正实数，且ρ0>ρ∞,p>0；

86、s43，转换跟踪误差

87、首先，归一化跟踪误差

88、

89、其中，μ(t)为转换后的无约束的误差，s(μ(t))为平滑且严格单增的转换函数。此外μ(t)还需保证：

90、

91、因此选择满足条件的误差转换函数s(μ(t))为

92、

93、转换误差μ(t)取

94、

95、至此，只要保证μ(t)有界，即可证明转换后的误差收敛，从而保证e1(t)在预设性能包络内。

96、所述的一种基于预设的形状记忆合金驱动器反步滑模控制方法，所述积分滑模反步控制，其积分滑模反步控制器的设计，其保证上述的预设性能控制过程中的转换误差μ(t)有界，同时有效实现三阶系统控制器的设计。其具体步骤如下：

97、s41，定义积分滑模面

98、首先定义积分滑模面函数s(t)：

99、

100、求导得到：

101、

102、将s33的转换误差式代入求导后的积分滑模面式得到：

103、

104、s42，选择趋近律

105、设计滑模指数趋近律

106、

107、联立趋近律和滑模面得到：

108、

109、进一步推导出x3得到

110、

111、s43，反步控制方法

112、其中x3为未知的状态量，根据反步控制原理，设虚拟控制量x3d和状态误差e2为：

113、e2(t)＝x3-x3d

114、设计lyapunov函数

115、

116、将上式求导：

117、

118、

119、将s15控制系统状态空间式代入到上式得到：

120、

121、s44，设计控制器

122、为了满足lyapunov稳定性定理，因此设计控制器u：

123、

124、5、稳定性和有界性分析

125、设lyapunov函数为

126、

127、将上式求导得到：

128、

129、将s41中滑模面导数和s43中误差导数代入上式得到

130、

131、随后，将式s42的x3表达式和s44的控制器代入上式得到：

132、

133、推导得到：

134、

135、因此，当r>0时，即可保证进而推导出系统渐进稳定。

136、此时，将s5的lyapunov函数代入到上式中得到：

137、

138、设c＝min{r,1}，得到

139、

140、v2≤qe-2ct

141、综上所述，其中q取任意常数，均可推导得出v2是有界的。s5可知滑模面s的有界性，s41滑模面方程中推导出转换误差μ(t)也是有界的。因此，闭环系统的跟踪误差e1(t)始终保持在预设性能的包络范围内，确保了系统的稳定性和精确性。

142、所述的一种基于预设的形状记忆合金驱动器反步滑模控制方法，所述材料学和机理模型，其整个驱动器材料学模型、机理模型、控制器和观测器进行仿真搭建，并且对输出角度进行跟踪测试，仿真工具采用matlab/simulink软件来验证该方法的可行性和有效性包括如下步骤：

143、s61，根据上述推导，搭建simulink仿真平台；

144、s62，测试系统在控制器和观测器作用下，观察驱动器输出角度与连续变化的目标角度的跟踪情况；

145、s63，测试系统在控制器和观测器作用下，观察驱动器输出角度与阶跃变化的目标角度的跟踪情况；

146、s64，测试系统在控制器和观测器作用下，观察驱动器输出角度与非线性变化的目标角度的跟踪情况；

147、s65，测试形状记忆合金驱动器在输入三种不同目标曲线下的误差约束情况；

148、s66，测试扩张状态观测器在驱动器输入三种不同目标曲线下的参数摄动与未建模扰动的观测效果。

149、本发明的优点与效果是：

150、本发明适用于空间薄膜可展结构中的驱动元件。采用形状记忆合金材料和偏置弹簧制成的驱动器，结合本方法中所提出的控制策略，能够达成精确的输出角度控制，从而有效地驱动空间薄膜可展结构。